万字长文带你了解双电层结构、电容和充电动力学

编审：Thor，Dysonian

近年来，人们在双电层(EDL)的理论建模方面取得了重大进展，这是电化学中的关键概念，对储能、电催化等技术应用十分重要。然而，在实际条件下理解电化学界面和充电机制的微观动力学仍然存在重大挑战。

近日，Chemical Reviews上发表了一篇题为“Understanding the Electric Double-Layer Structure, Capacitance, and Charging Dynamics”的综述，该综述深入探讨了用于描述电容储能的电化学系统EDL结构和电容平衡和动态响应的理论方法，还特别强调了最近的进展，旨在捕捉非经典的EDL行为，如振荡离子分布，非金属电极的极化，电荷转移，以及电极与有机电解质或离子液体界面的微孔中各种形式的相变。这一综合分析从理论上阐述了材料特性和电化学性能之间的可预测关系，并为进一步发展电化学系统的合理设计和优化提供了机会。

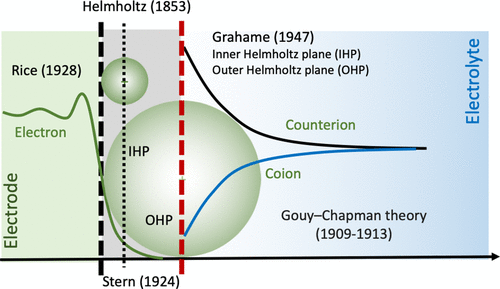
图1. 双电层（EDL）的经典模型。@ACS

图1显示，Helmholtz提出的EDL模型由两个具有相等但相反电荷的数学平面组成，一个代表电极表面，另一个代表反离子。两个平行平面（即双层）之间的间隔与反离子半径相当。EDL电容器通常由多孔电极和浓缩电解质或离子液体制成，以使总电容最大化，称为超级电容器。

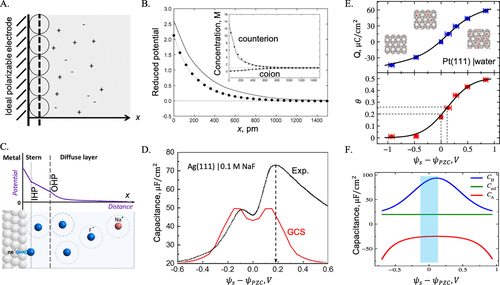
图2. A.理想可极化电极（IPE）附近离子分布的Gouy-Chapman-Stern（GCS）模型示意图。B.GCS理论与蒙特卡洛（MC）模拟的比较。C.在金属-电解质界面处具有部分电荷转移的格雷厄姆模型。D.GCS理论与不同表面电位下0.1 M NaF溶液中银金属实验电容的比较（ψ_s)。E.从头计算的分子动力学（MD）模拟计算出Pt（111）表面化学吸附水分子（θ）的表面电荷密度（Q）和覆盖率。F. 将亥姆霍兹电容CH分解为溶剂电容C_sol和化学吸附电容CA。@ACS

图2A显示，Gouy-Chapman（GC）理论对应于将泊松-玻尔兹曼（PB）方程应用于对称电解质，其靠近具有均匀电荷密度Q的平面。如果EDL由均匀介电介质中与一价带电硬球接触的平面壁表示，则GC理论产生的局部电势和离子分布即使在中等离子浓度下也与仿真数据相当吻合。例如，图2B将理论预测与蒙特卡罗（MC）仿真进行了比较。当本体中的离子浓度高达2 M时，GC理论预测的离子密度分布接近定量。然而，局部电势显示出更显著的差异，表明离子密度曲线的良好一致性部分是由于误差的消除，即由均场近似高估的局部电势被离子排除的体积或尺寸效应部分补偿。如果系统包含多价反离子，则GC预测和模拟结果之间的差异是巨大的。

PB方程忽略了离子和溶剂的分子性质。此外，它仅考虑了均场水平上均匀介电介质中的库仑相互作用。由于EDL的维数大多是微观的，因此PB方程预测的属性可能与对应于实际电化学界面的属性产生显着偏差。多年来，人们通过考虑介电不均匀性或结合静电相关性来改善PB方程。由于许多理论工作都致力于点电荷模型，因此它们对通常用于电容式储能的浓缩电解质的影响有限。即使对于稀电解质溶液中的近理想电极（例如，与NaF溶液接触的Ag（111）），GCS理论也只有在假设stern层介电常数随局部电场变化时才产生合理的EDL电容。最近的ab initio MD模拟表明，水分子在Pt（111）表面的特异性吸附可能导致负电容响应（图2F）。理论分析和实验数据表明，除了局部溶剂效应外，为了描述特定的离子吸附，还必须考虑部分电荷转移（图2D）。虽然PB方程可以根据经验进行修改，以包括水重组和非电静力离子-表面相互作用，但仍需要第一性原理方法来描述离子物质或溶剂分子的化学吸附。

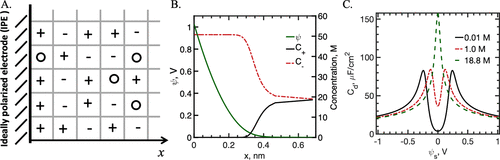
图3. EDL作为晶格气体。A.离子（±）和溶剂分子（○）随机放置在平面电极（IPE）附近的立方晶格上。B.由均场晶格-气体模型预测的局部电势ψ（x）和离子浓度。C.差分电容与晶格模型预测的表面电位的关系。@ACS

图3A显示了理想可极化电极（IPE）附近EDL的晶格，即与电解质接触的完美金属，在界面处没有电荷转移。根据均值场近似，亥姆霍兹能量包括一个与PB方程给出的静电分量相同的静电分量，以及一个熵贡献，以解释晶格上化学物质的随机排列。图3B和C给出了晶格模型预测的EDL结构和电容。就像GC理论预测的那样，当远离带电表面时，局部电势单调地衰减。然而，不可压缩性的假设导致电极表面附近离子密度的饱和。所谓的空间位阻效应也可以通过在漫反射层之前添加“凝聚”区域来捕获。与GC理论预测的U形不同，差分电容分别在高离子浓度和低离子浓度下响应电极电压的变化而显示“钟形”和“骆驼”形。

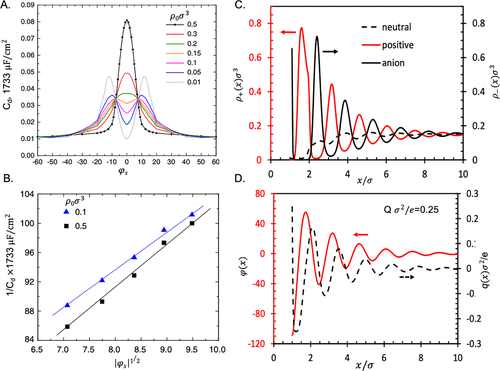
图4. EDL结构和电容由电解质的原始模型预测。A. 不同体积浓度下有机电解质的差分电容与降低的表面电位，ρ0σ3，其中σ = 0.6 nm是离子直径。B.高表面电压下差分电容的平方根反比衰减。C.电荷密度Qσ表面附近离子液体的阳离子和阴离子离子密度降低2/e = 0.25。在这里，每个阳离子被描述为切向连接的正球和中性球的二聚体。D.降低的局部电势，φ（x）和积分电荷密度q（x），对应于面板C。@ACS

晶格模型预测的局部离子浓度的饱和效应没有得到基于粒子的模型或实验所证实。图4显示，强烈的静电相关性和排除体积效应可能导致振荡的离子密度曲线和局部电势，而均场近似无法捕获这些因素。格子气体模型可以通过使用弗洛里-哈金斯型方程来推广到具有不对称离子物质的电解质。Zhang和Huang等人比较了几种解释尺寸不对称的方法，并从晶格构型数，无量纲过量化学势和差分电容的角度讨论了它们的物理意义。改进的PB方法能够捕获具有强静电相互作用系统的过筛效应。然而，他们预测的离子密度分布和局部静电势与基于粒子的模型产生的明显不同。均场方法的一个主要优点在于它们在捕获电容式储能的一般特征和描述离子系统中的各种相变（包括电压诱导电荷分离，溶剂解混和面内结构排序）方面的简单和高效。

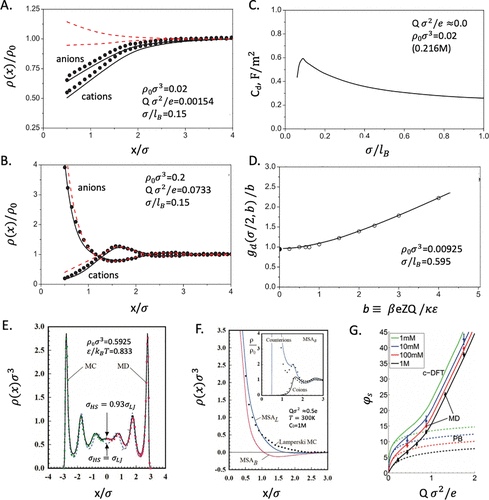
图5. 由电解质基元模型预测的平面EDL。A和B.离子密度曲线的cDFT和MC的比较。C.EDL电容随温度降低而变化（σ/l_B)。D.cDFT和MC的比较，以测定阳离子和阴离子的接触密度之间的差异。E.根据MC和MD计算的狭缝孔隙中Lennard-Jones（LJ）流体的局部密度与cDFT的比较。F.由不同版本的cDFT预测的离子密度曲线。G.三个EDL模型预测的表面电势的比较。@ACS

图5比较了多个版本的经典密度泛函理论（cDFT）（MSAB，MSAL和ccDFT），其中包含EDL电容、不同平面附近离子分布以及表面电位对表面电荷密度的依赖性的仿真结果。虽然通过选择自由能函数可以达到与仿真结果一致，但它们的差异是显着的，特别是在静电相关效应作用下。尽管第二个接触值关系并不准确，图5D表明，它预测了接触时阳离子和阴离子浓度之间的差异，与ccDFT预测非常一致。有趣的是，ccDFT预测了差分电容在响应温度变化时的非单调依赖性（图5C）。在MC仿真和实验中都观察到类似的趋势，但传统的EDL模型无法预测。只有当带电表面附近的静电相关性和离子分布得到充分描述时，双层电容的非单调温度依赖性才能再现。

应该注意的是，cDFT不仅对硬球系统有用。该理论过程同样适用于更接近实际的EDL模型，包括那些含有有机电解质和具有复杂分子结构的离子液体模型。例如，图5E-G将模拟数据与cDFT和PB方程进行比较，用于由带电Lennard-Jones(LJ)球体组成的模型EDL。虽然cDFT和仿真结果显示出优异的一致性，但PB方程在高盐浓度下不能产生定量性能。它也不能预测强带电表面附近的精确离子分布。

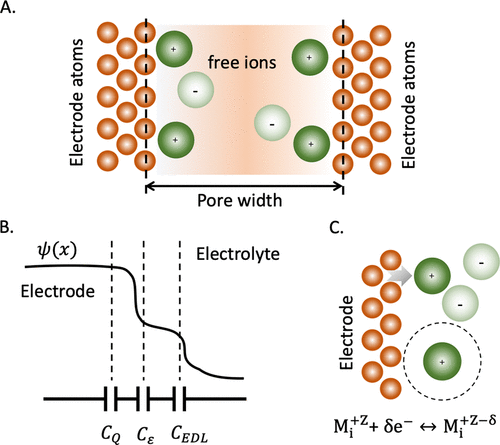
图6. A. 多孔电极中电解质溶液的示意图，定义为开放系统，即具有固定的电子(μ_e)、溶剂分子(μ_s)和离子物质(μ_±)化学势的系统。B.局部电势和对总电容的各种贡献：量子（C_Q），电介质（C_ε）和漫反射层电容（C_EDL).C.电极原子之间的电荷转移（M_i）和由法拉第反应表示的吸附离子。@ACS

假设在电极-电解质界面（即IPE）上没有电子转移，并且电极原子的位置被冻结，EDL可以用电子，离子物质和溶剂分子的开放系统来表示，如图6A所示。电子化学势μ_e不仅通过电极的表面电位，而且通过电子结构和状态密度的变化来影响能量存储。后一种贡献分别导致量子电容（C_Q）和介电电容（C_ε）的出现，如图6B所示。如果电荷转移发生在电极-电解质界面，则必须考虑额外的贡献来解释吸附物质的电子结构和表面反应（图6C）。

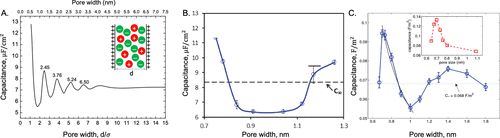
图7. 电容对狭缝孔隙中离子液体孔径的依赖性。A.基于碳孔中模拟EMIM-TFSI的受限基元模型，cDFT预测的1.5 V时的积分电容。B.根据MD模拟，离子液体粗粒模型的积分电容随狭缝孔宽的变化。在这里，C∞表示开平面电极的电容。C.来自全原子MD仿真的EMIM-TFSI在1.41 V碳狭缝孔隙中的积分电容。插图显示了相应的实验结果。@ACS

图7A显示，cDFT计算预测了电容对孔隙宽度的振荡依赖性。当孔径接近离子直径时出现最大电容，这与实验报告的电容异常增加非常吻合。利用原子模拟，Wu等人在考虑离子结构和电极原子的极化性的情况下，研究了纳米孔中离子液体的EDL结构。仿真结果在图7B中重现，该图显示，电容对孔隙宽度的依赖性呈现U形曲线。当模拟较大的狭缝孔隙时，振荡曲线变得明显。图7C显示电容表现出两个峰，分别位于0.7和1.4 nm，与离子直径相匹配。第一个峰从0.7衰减到1nm，与实验结果一致。随着孔径从1.0增加到1.8 nm，第二个峰的出现证实了cDFT预测的振荡行为。

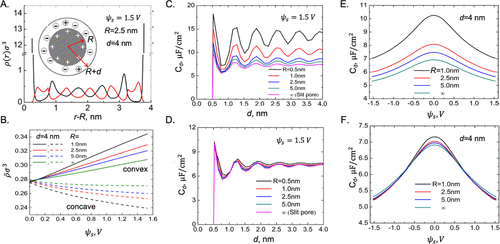
图8. EDL的球壳模型。A.cDFT预测的阳离子和阴离子密度曲线。B.球壳内反离子和共离子在不同曲率和表面电位下的平均密度。C和D：孔径对凸（C）和凹面（D）表面积分电容的影响。E和F：孔径对凸（E）和凹面（F）表面差分电容的潜在影响。@ACS

通常，具有弯曲边界的微孔促进正负离子的分离，产生更高的电容。离子偏析和电容增加的大小取决于曲率以及施加的电位。综合效应可以用Lian等人提出的通用模型来表示，该模型同时考虑了孔径和曲率效应。如图8A所示，限制在球壳中的离子液体局部密度表现出类似于狭缝孔中的振荡曲线。然而，孔隙曲率对阳离子和阴离子的平均密度之间的差异有很大的影响（图8B），这解释了随着曲率的增加，电容的显着改善。此外，曲率增强了电容随孔径的振荡变化（图8C）。有趣的是，电极-电解质界面的凸面和凹面几何形状显示出不同的曲率效应（图8D）。在前一种情况下，电容随着界面变得更加弯曲而上升，但这种效应在凹面附近几乎不存在。随着曲率的增加，差分电容在凸面附近也显示出显着的改善。然而，如果表面凹陷，这种影响是微不足道的（图8E和F）。

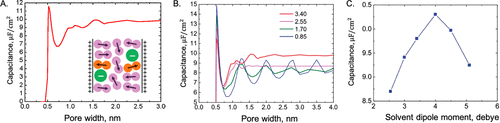
图9. 通过cDFT预测溶剂效应。A.纳米多孔电极在1.5 V下的积分电容随孔径的变化。B.溶剂极性和电极孔径对有机电解质积分电容的综合影响。C.积分电容随溶剂偶极矩的变化。@ACS

使用cDFT和有机溶剂二聚体模型，Jiang和Wu研究了纳米狭缝孔中有机电解质(TEA-BF₄/ACN)的电容。如图9A所示，当孔径与离子直径相当时，除了由于脱溶而产生的尖锐峰外，电容随孔径的变化很小。这种趋势与从实验中观察到的趋势没有太大区别。与离子液体电容对孔径的强烈振荡依赖性形成鲜明对比的是，峰值与大孔隙极限处的峰值没有显着差异（图9B）。当溶剂偶极矩足够大时，电容接近恒定，因为EDL结构主要由反离子和高度有序的溶剂分子组成。极化溶剂分子破坏了带电表面附近阴离子-阳离子层的交替，从而抑制了电容随孔径的振荡。图9C显示了溶剂极性对具有不同偶极矩有机电解质的影响。火山形曲线表明，通过调整溶剂的偶极矩，可以使电容最大化。

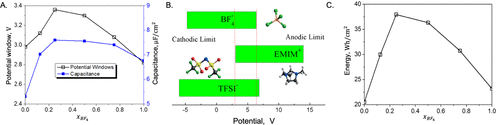
图10. 增强采用离子-液体混合物的超级电容器电容性能。A.工作电位窗口（OPW）和积分电容随BF₄在EMI-TFSI/EMI-BF₄混合物中摩尔分数的变化。B.OPW与单个离子的阴极/阳极极限之间的关系。C.离子-液体混合物中能量密度随EMI-BF₄中BF₄摩尔分数的变化。@ACS

将离子液体与其他离子液体或助溶剂混合会改变本体性质，如扩散率、粘度和导电性。此外，离子-液体混合物可能具有优异的工作电位窗口（OPW）和长循环性能。结合实验研究和第一性原理计算，cDFT预测可以确定最佳成分，以最大化EDL电容，同时具有扩展的OPW和增强的离子动力学。例如，Lian等人研究了由一种普通阳离子和两种不同大小的阴离子组成的离子-液体混合物的电位窗口，界面结构，电容和能量密度。如图10所示，理论结果表明，电容随离子组成而非线性变化。EmimTFSI/EmimBF₄混合物的电容最大值大约在4：1的比例。这种效应可归因于分层结构的显着减少以及由于存在较小的BF₄^–阴离子而导致电极表面上Emim⁺反离子的接触密度增强。

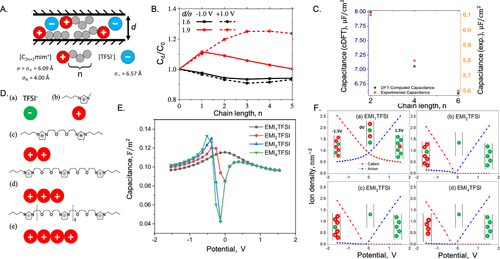
图11. A.由咪唑阳离子与TFSI阴离子配对的离子液体的示意图。B.归一化积分电容与阳离子烷基链长度的关系。C.电容与烷基链长度的理论和实验值的比较。D.由相同带电粒子的切向连接链表示的低聚阳离子。E.差分电容随低聚离子液体施加电位的变化。F.宽度为d=0.8nm的纳米孔内寡聚阳离子和单体阴离子的平均密度数。@ACS

在超级电容器中使用离子液体的一个主要优点是可以选择广泛的阳离子和阴离子来优化器件性能。cDFT用于研究阳离子侧链对碳电极微孔中咪唑基室温离子液体电容的影响。图11A的理论结果表明，在中等电极电位下，通过将中性链段连接到阳离子上可以增加电容（图11B）。然而，中性链段可能会对具有大微孔或高电位的电极的电容产生负面影响（图11C）。侧链效应的相反趋势反映了中性链段的共离子耗尽（正面效应）和阳离子整体尺寸的增加（负面影响）之间的竞争。

图11D显示了一种类似的粗晶模型，用于研究纳米多孔电极中低聚离子液体（OIL）的电容性能。与应用于场效应晶体管相比，纳米多孔电极中OIL的电容性能对充电电位敏感（图11E）。可以通过考虑纳米孔内阳离子和阴离子的平均密度来理解充电曲线（图11F）。在低电极电位下，阳离子和阴离子与表面电位的平均密度接近对称，这表明孔隙中的共离子（阳离子）与来自本体的反离子（阴离子）交换。在这种情况下，差分电容急剧下降，因为离子吸附在小电势下变得饱和。在高电极电位下，共离子从孔中耗尽，充电过程以反离子插入为主，这导致差分电容的下降速度较慢。与单体离子液体不同，几乎没有低聚阳离子，只有少数阴离子以低电荷电位进入纳米孔。当表面电位的绝对值增加时，随着更多的反离子从本体转移到孔中，差分电容上升。电极电位的进一步增加导致纳米孔内反离子的饱和，表现为差分电容下降。因此，差分电容-电位曲线呈现出“骆驼形状”，这与单体离子液体的“钟形”形状不同。

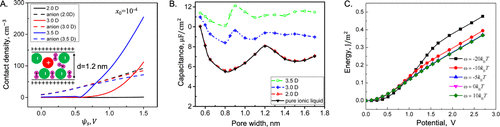
图12. 使用极性添加剂增强电容性能。A.阴离子和添加剂分子的负段的接触密度与表面电势的关系。B.纯离子液体及其与不同偶极矩添加剂的混合物的积分电容与孔径的关系。C.单位表面积的能量与不同表面能(ω)的杂质外加电势的函数关系。@ACS

超级电容器的性能对电极-电解质界面处的离子分布很敏感，可以通过向电解质中添加化学物质或在存在杂质的情况下轻松改变离子分布。图12显示了杂质对表面浓度、电容和能量密度的一些可能影响。在这里，cDFT计算基于离子液体的原始模型，其中杂质分子由带相反电荷的球形二聚体表示。图12A显示，杂质分子的接触密度可以达到400 M，甚至其在本体中的摩尔分数也只有x₀=10^–4。结果，杂质对电容和能量密度有剧烈影响（图12B和C）。理论预测表明，添加剂可以显著增加EDL电容和能量密度。

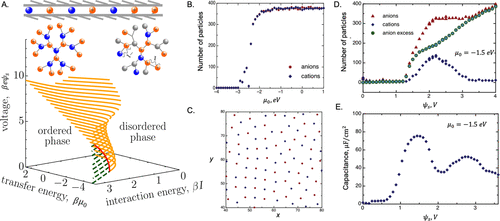
图13. 限制在导电壁之间的离子流体二维（2D）示意图。A.Bethe晶格模型根据离子转移能(βμ₀)、离子-离子相互作用能(βI)和施加电压(βeψ_s)预测有序无序跃迁。B.通过大正则蒙特卡罗模拟预测中性狭缝孔隙中的离子吸附到。C. 离子电化学势μ₀=1 eV的模拟快照。D.狭缝孔隙中的离子吸附与施加电压的关系。 E.图D中狭缝孔隙系统的差分电容。@ACS

例如，图13A显示了由经典spin-1 Blume-Capel(BC)模型预测的完整相图。它预测2D系统可能表现出一阶，二阶相变（图13A）。从定性上讲，早期的均场理论预测了单层离子物种中可能的相变，该理论解释了二维离子-离子相互作用和图像效应。随后的MC模拟明确考虑了筛选的库仑相互作用，表明中性狭缝孔的离子吸附遵循Frumkin等温线（图13B和D），但吸附对表面电位的响应是非单调的，导致电容呈现 “双骆驼”形状（图13E）。模拟结果显示，从类气体结构到“类玻璃”结构的转变过程中波动增强，表明可能存在BC模型预测的相变。在零电压下，阳离子和阴离子自组织成一个方形晶格（图13C），用于限制在两个平行石墨壁之间的1，3-二甲基氯化咪唑鎓离子液体的液固转变。有趣的是，电容在电压正（图13E）和负两侧都表现出两个最大值。双骆驼曲线可归因于导致高电压下共离子耗尽的亲离子效应。

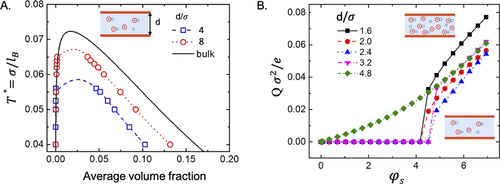
图14. A.模型离子流体在体相和两个中性狭缝孔中的相图。B.表面电荷密度随不同宽度狭缝孔隙中表面电压的变化。@ACS

图14显示，孔径限制导致气液共存区域变窄，并且随着孔径的减小，临界温度和临界密度都会降低。相变导致表面电荷对电势的依赖性的不连续性以及临界点处电容的发散。除了狭缝和圆柱形孔外，离子-蒸汽-液体转变可能发生在无序的多孔基质中。虽然单孔模型对于实际电极进行了过度简化，但预计毛细管冷凝的定性行为与孔隙形状和尺寸分布无关。

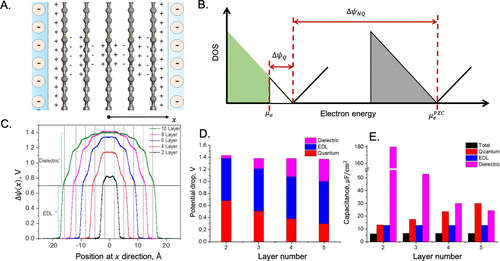
图15. A.由与电解质溶液接触的几个石墨烯层组成的模型电极。B.零电荷电位和正表面电荷时的状态密度（DOS）示意图。C. 在9 μC/cm²的相同表面电荷密度下，由Joint-DFT预测的不同层石墨烯在6 M水系电解质中的局部电势。D. 将电位降分解为模型电极的量子、电介质和EDL贡献。E.相应的电容贡献。@ACS

量子电容与电极的电子密度响应于电压的变化有关，这可以通过由与电解质溶液接触的几层石墨烯组成的模型电极来说明，如图15A所示。图15B显示，刚性带近似（RBA）假设电子状态密度（DOS）的形状与电极电压不变。虽然RBA允许在零电势（p_zc）下计算来自DOS的电极电荷，但它没有考虑充放电对局部电势和电荷分布的影响。极化效应包括电子和电解质的贡献，表现在局部电荷分布中。电势的变化随后可用于分别定义介电电容和EDL电容（图15C和D）。

图15E说明了Joint-DFT预测的总电容的各种分量。结果表明，随着石墨烯层数从2个增加到5个，介电电容单调下降。量子电容的趋势相反，而扩散层的EDL电容保持不变。对于所考虑的特定系统，扩散层主导总电容，但量子和介电贡献显然是不可忽视的。

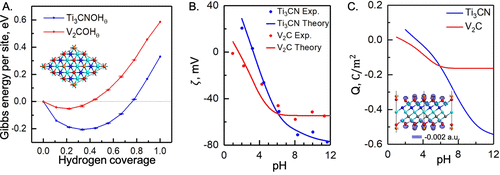
图16. A.由Joint-DFT预测的在氢原子（θ）不同表面覆盖处的两个中性MXenes形成吉布斯能。B.zeta电位的pH依赖性，C.cDFT预测的MXene表面电荷密度。@ACS

图16显示了通过互补第一性原理和cDFT计算预测的MXenes原子结构和表面电荷。这里基于 Joint-DFT 的第一性原理方法允许预测中性状态下的MXene基。同时，结合表面反应的微动力学模型，cDFT可用于预测表面电荷和组成，以响应电极电压和溶液条件。

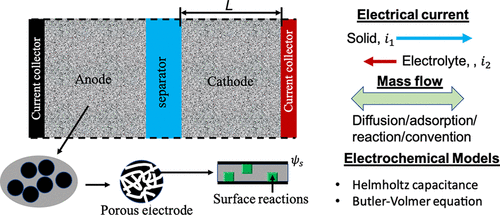
图17. 用于电容式储能的电化学电池示意图。@ACS

图17显示，用于电容式储能的电化学电池由两个多孔电极组成，一个正极和一个负极，被电解质包围。从宏观角度看，多孔电极可以用平均孔隙率ρ，比表面积θ和有效电导率K₁来表征。经典的多孔电极理论假设所有动态变量都可以用平均量来表示，这些平均量仅在垂直于电化学电池的方向上变化。充电动力学通常根据电流和电极电压之间的定量关系来描述。。经典的多孔电极理论提供了一个强大的数学框架来描述电极过程的动态行为，包括局部电解质浓度的演变。它通常用于分析电极孔隙率、电导率和表面反应对各种充电模式的影响。然而，宏观过程采用大量半经验参数，并对电容过程进行严格的假设。

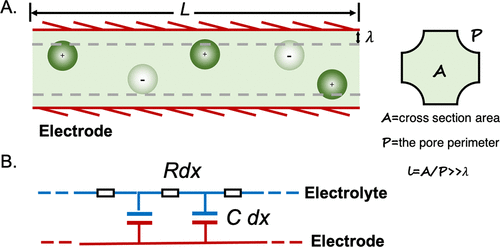
图18. A. 含有稀电解质的直孔示意图。B.当德拜长度λ远小于孔径时，充电动力学可以用传输线模型表示，每单位长度的电阻和EDL电容被视为常数。@ACS

离子传输和电荷动力学的分子理论主要基于泊松-能斯特-普朗克（PNP）方程。线性化NP方程有利于理解任意形状的直孔充电动力学（图18）。另外，假设（i）电极是完美的导体;（ii）孔径远大于德拜筛选长度λ，并且（iii）EDL电容是由C_d=ϵ/λ给出的常数，线性化NP方程预测电解质中的电势(ψ)和电极的表面电荷密度(q)根据扩散方程响应施加的电势

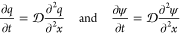
其中x代表孔隙长度方向上的坐标，是孔隙的横截面积和孔隙周长的有效扩散率。对于直孔，等于孔体积除以其表面积。

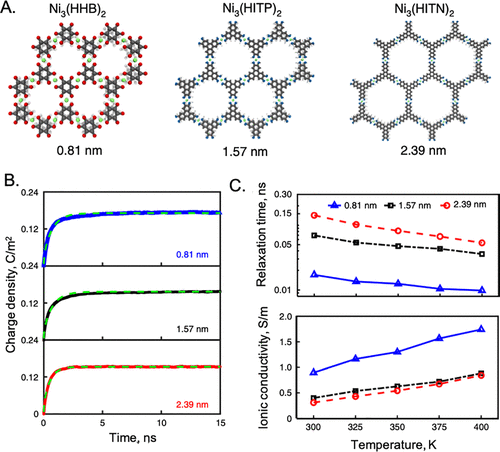
图19. A.三个MOF电极中准1D孔的原子结构。B.[EMIM][BF₄]离子液体中，400 K下，MOF正极(ψ_s=4 V)单位表面积的电荷密度演变。C.不同温度下MOF孔隙中离子液体的固有弛豫时间和离子电导率。@ACS

图19显示了离子液体中金属有机骨架（MOF）电极的充电动力学。将TL弛豫时间作为可调节参数，TL模型能够在宽的温度范围内以高达4 V的施加电位拟合MD模拟数据。值得注意的是，与实验相比，它产生了合理的弛豫时间。离子电导率由弛豫时间和对应于电极电位的恒定EDL电容计算而得。图19C显示，TL模型预测离子电导率随着孔径的减小而增加，这是因为由于孔壁诱导的图像电荷增强了对静电相互作用的筛选。有趣的是，由于面内结构转变，MD模拟还揭示了充电速率和孔径之间的非单调关系。在早期的工作中，Kondrat和Kornyshev证明了扩散方程也适用于模拟具有单层离子液体的金属孔充电动力学。在这种情况下，由于金属壁的电子极化率，扩散系数被修正，以反映屏蔽的离子-离子相互作用。

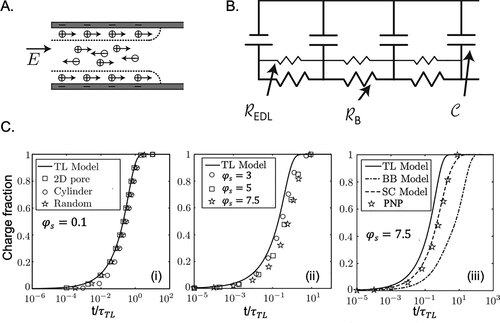
图20. A.电极孔中心和表面区域的离子运动示意图。B.用于描述单个孔隙的充电动力学的传输线模型。C.充电分数Q(t)/Q₀与在恒电位充电过程中减少的充电时间(t/τ_TL)的关系。@ACS

图20将PNP方程的数值结果与de Levie模型的预测及其最近的修正模型进行了比较。de Levie模型能够在低充电电位（φ_s=0.1或ψ_s∼2.5 mV）下再现三个不同形状的直孔充电动力学，与PNP方程非常一致。在稍高的电势下，de Levie模型表现得相当好，因为电荷分数对施加的电势相对不敏感。在无量纲电位φ_s=7.5或ψ_s∼200 mV 时，表面传导(SC)，即扩散层内离子传输引起的电流变得更加重要。虽然SC模型重现了PNP方程的数值结果，但de Levie模型低估了充电时间，而BB模型则高估了充电时间。

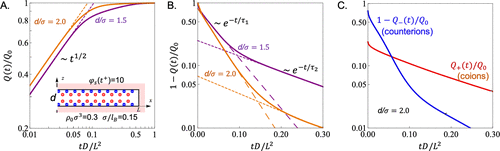
图21. 通过TDDFT预测的浓缩电解质溶液中狭缝孔在充电早期(A)和晚期(B)阶段的电荷演化。C.阳离子和阴离子对总孔电荷的贡献。@ACS

TDDFT第一次被Aslyamov等人用于研究有机电解质溶液中多孔电极的充电动力学。如图21所示，模型系统由与受限基元模型（RPM）表示的电解质溶液接触的狭缝孔组成。TDDFT预测，总电荷的演变在充电的早期阶段遵循指数1/2的幂律演变，然后在后期出现连续的指数衰减（图21A和B）。对于浓缩电解质溶液中的纳米孔充电，TDDFT预测电荷弛豫在后期明显减慢。在后期阶段，缓慢的充电归因于反离子浓度的增加导致的共离子释放受阻。由于拥挤效应，反离子吸附和共离子释放密切相关。

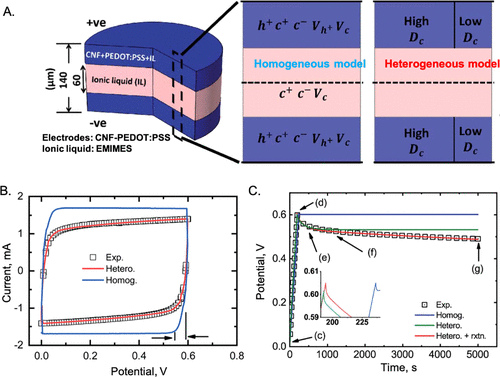
图22. 使用PNP方程模拟导电聚合物超级电容器的动力学。A.均相和非均相模型中使用的电化学电池和参数示意图。B.用均相和非均相模型拟合循环伏安图。C.理论和实验中自放电电位的比较。@ACS

图22显示了最近模拟导电聚合物超级电容器的循环伏安图（CV）和自放电电位。使用导电聚合物中的空穴和离子液体中离子物种的点电荷模型，并假设电极-电解质界面处的体积电容恒定，PNP方程能够描述各种实验数据，包括充电动力学 超级电容器和自放电特性和阻抗谱。聚合物电极的电荷载流子（即空穴）本质上是PB方程所假设的点电荷。此外，由于阳离子和阴离子之间的强结合，离子液体可以被描述为稀电解质。这些因素解释了为什么PNP方程能够很好地表示离子液体中导电聚合物的充电行为。

图23. A.EDL电池的示意图和相应的等效电路模型。B.充电早期（φ_s=-10）期间阳极附近阳离子密度的演变。C.不同施加电位下表面电荷的衰减。@ACS

图23显示了同一平行电极系统局部反离子密度和表面电荷密度的演变，但电解质溶液由基元模型表示。虽然稀溶液理论预测弛豫时间与施加的电位无关，但TDDFT计算表明，随着表面电位的增加，充电时间会减少。响应时间的单调性降低是可以预见的，因为较高的电极电压会导致更强的电场，从而加速离子运动。有趣的是，TDDFT预测弛豫时间取决于大电位下的电解质浓度。与EC模型所预测的不同，响应时间首先随着电解质浓度的增加而上升，而在大离子浓度下由于EDL厚度的减小而下降。

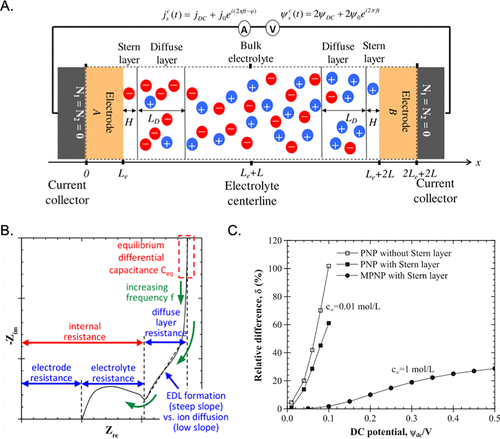
图24. A. 使用MPNP方程模拟的EDL电池示意图。B.奈奎斯特图的物理解释。C.EIS和双层电容之间的相对差异。@ACS

图24显示了EDL电池的示意图。结合电极和电解质的欧姆定律，MPNP方程用于描述电化学阻抗谱（EIS），循环伏安法（CV）和恒流循环曲线（GC）。图24B和C根据EDL模型解释了典型奈奎斯特图的物理含义，并比较了同一模型预测的EIS和平衡电容。EIS测量高估了稀释电解质溶液的EDL电容，而低估了受大电势影响的浓缩电解质溶液EDL电容。基于物理场的数值模拟有助于识别EIS测量的固有局限性。

图25. A.用于在离子液体中进行EDL充电的电化学电池模型。B.平衡表面电荷密度与cDFT预测的电池宽度的关系。C.不同电池宽度的表面电荷密度随时间的演变。D.MD模拟的离子分布快照。E.正极的平衡表面电荷密度随电极间距的变化。F.施加1.0 V偏压后，MD预测的不同电池宽度下的充电动力学。@ACS

图25显示了TDDFT预测的位于两个平行电极之间的模型离子液体的表面电荷的演变。平衡表面电荷随电池厚度的振荡变化来自阳离子和阴离子的远距离逐层分布。然而，在两个电极之间施加电压时，TDDFT预测的表面电荷随时间的演变与仿真结果明显不同。图25显示，TDDFT预测了在平衡条件下可能出现的三种充电过程，对应于正常、振荡和电荷反转。然而，在MD模拟中，这种过程不太明显。另外，TDDFT和MD都不会产生稀溶液模型所预测的充电曲线指数衰减。

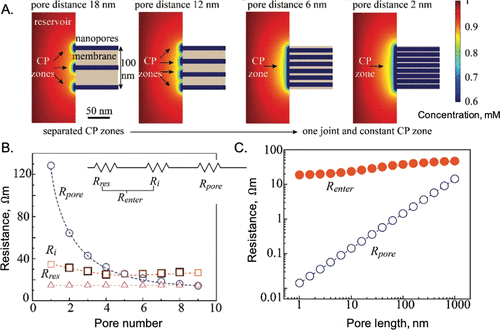
图26. 入口对纳米孔中离子传输的影响。A.PNP方程预测的阴离子浓度显示浓度极化(CP)区域随着孔间距的下降而收敛。B.储存阻力(R_res)、界面阻力(R_i)和孔隙阻力(R_pore)与狭缝孔数量的关系。C.孔长对电阻的影响。@ACS

Gao等人通过数值求解二维PNP方程，研究了离子通过单个纳米孔和多个平行孔传输的入口效应。图26A显示，当孔间距与孔宽度相当时，入口附近的浓差极化(CP)区会聚成一个联合过渡区。虽然孔电阻与孔长度呈线性关系，并随着孔数量的增加而成比例减小，但入口阻力(R_ent)对孔长度和数量密度相对不敏感（图26B和C）。

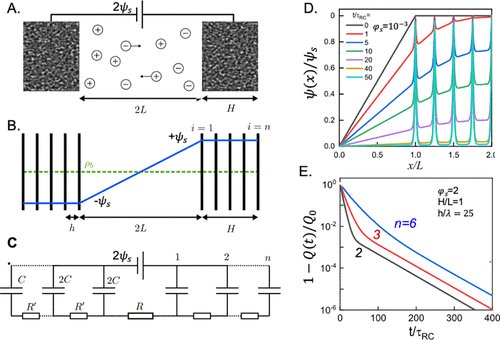
图27. A.由长度为2L的停滞扩散层隔开的两个多孔电极示意图。B.每个电极由等间距(h)的平行金属片表示。C.传输线(TL)模型。D.在小施加电压和低电解质浓度下降低电势的演变。E.大施加电压下总电荷的演变。@ACS

为了介绍孔隙结构对充电行为的影响，Lian等人提出了一种包含许多相等间距（h）的平行金属片电极模型。这些金属片可进行离子扩散，并同时允许施加电势。如图27所示，线性化PNP方程的数值结果证实了，在小电压下，金属片进行恒电位充电。然而，在大电压下，电荷密度表现出双指数衰减（图27E），早期的弛豫由τ决定。

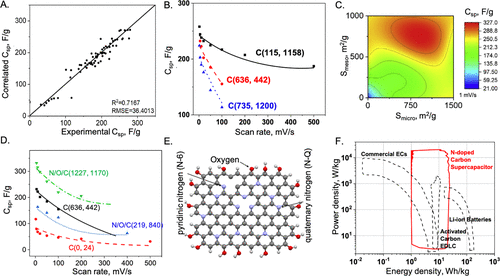
图28. A.6 M KOH水溶液中活性炭比电容的实验数据与人工神经网络(ANN)的相关性。B.与实验数据相比，比电容与扫速的ANN预测。C.比电容与ANN预测的微孔和中孔表面积的关系。D.具有不同表面成分的N/O共掺杂碳比电容与扫速的ANN预测与实验数据的比较。E.ANN模型预测的N/O共掺杂碳电极优化结构。F.由N/O共掺杂碳电极制成的超级电容器Ragone图。@ACS

对于现实的电极，微观结构的不确定性几乎是不可避免的，它们的实际使用主要取决于远离平衡条件下的动态过程。为了量化EDL的充电行为和非平衡特性，机器学习(ML)方法成为一种基于物理建模的有效方案。例如，人工神经网络(ANN)用于将超级电容器的电化学性能与扫速和碳电极的各种特性相关联（图28）。ML模型能够解释氮和氧掺杂的协同效应，并确定导致更高能量和功率密度的碳电极结构特征。

本文所讨论的EDL模型多种多样，原则上，平衡模型可以通过与动力学相关的传递方程相结合来扩展，以描述时间依赖性现象。此外，当有大量数据可用时，机器学习（ML）方法可以量化EDL的充电行为和非平衡特性。由于无数的化学事件可能发生在电极-电解质界面或电极的微孔内，因此每个EDL模型都反映了某些实际情况。但为了描述EDL在现实条件下的行为，需要更复杂的模型。本文分析了近年来描述非经典EDL结构和充电行为（如振荡离子分布、界面相变和非局部电荷转移）的理论进展，还讨论了各种EDL模型的关键假设，并阐明了它们在电容式储能中的应用。虽然很难对不同的模型进行直接比较，因为它们的范围和复杂性各不相同，但本文分析了它们表示热力学非理想特性的优点和局限性。与EDL的平衡特性相比，能量存储和电荷转移背后的动态行为仍然鲜为人知。由于多孔电极的复杂性，单孔分析通常不足以描述与实际电化学器件相关的离子输运和表面反应。此外，人们可能会质疑原始模型对微孔中电荷转移和离子传输的适用性。目前尚未开发可靠的理论工具来描述量子动力学和经典动力学在非平衡条件下电化学系统的耦合效应。由于这些原因，ML方法的进一步应用有望将电化学系统的性能与材料特性和运行条件相关联。数据驱动的方法不仅可用于捕获电极以及电解质的固有特性，而且可用于预测EDL在平衡和动态测量方面的性能。有了足够的实验或理论预测数据，结合基于物理的模型和ML方法将能够提取输入和输出变量之间的定量关系。

Jianzhong Wu*. Understanding the Electric Double-Layer Structure, Capacitance, and Charging Dynamics. Chemical Reviews. 2022.

DOI:10.1021/acs.chemrev.2c00097

声明：本文仅代表作者观点，如有不科学之处，请在下方留言指正！文章系作者授权新威公众号发布，转载及相关事宜请联系小威（微信号：xinweiyanxuan）。